
Diketahui bentuk standar dari f(x,y) = x’, Bentuklah menjadi SOP, Sebelumnya harus mengingatkan kembali hukum-hukum aljabar Boolean, Nah…pertama f(x,y) = x’ kita gunakan hukum identitas sehingga menjadi f(x,y) = x’.1, 1 dalam hal ini adalah hukum identitas, Selanjutnya kita gunakan hukum komplemen, sehingga menjadi f(x,y) = x’ . (y + y’), y + y’ adalah hukum komplemen yang hasilnya 1, Kemudian kita gunakan hukum distributif sehingga menjadi f(x,y) = x’y + x’y’, Sehingga kita mendapatkan bentuk standarnya yaitu f(x,y) = x’y’ + x’y dan bentuk kanonik f(x,y) = Σm(0, 1)

Contoh berikutnya yaitu mencari bentuk Maxterm nya, Diketahui bentuk standar dari f(x,y) = x’, Bentuklah menjadi POS, Pertama-tama karena ini awalnya fungsi booleannya adalah SOP maka kita lakukan terlebih dahulu invers nya, Yaitu menjadi f’(x,y) = x, Pertama f’(x,y) = x kita gunakan hukum identitas sehingga menjadi f(x,y) = x.1, 1 dalam hal ini adalah hukum identitas, Selanjutnya kita gunakan hukum komplemen, sehingga menjadi f’(x,y) = x . (y + y’), y + y’ adalah hukum komplemen yang hasilnya 1, Kemudian kita gunakan hukum distributif sehingga menjadi f’(x,y) = xy + xy’, apakah fungsi boolean tersebut sudah selesai..?, Ternyata kita harus inversi-kan lagi…
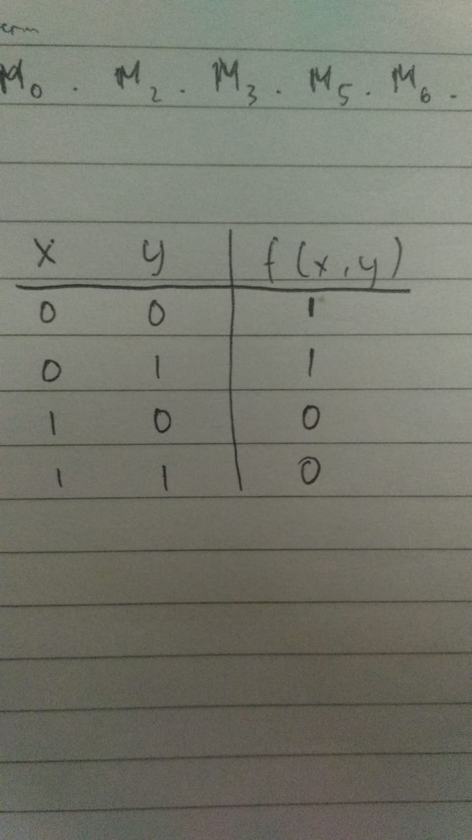
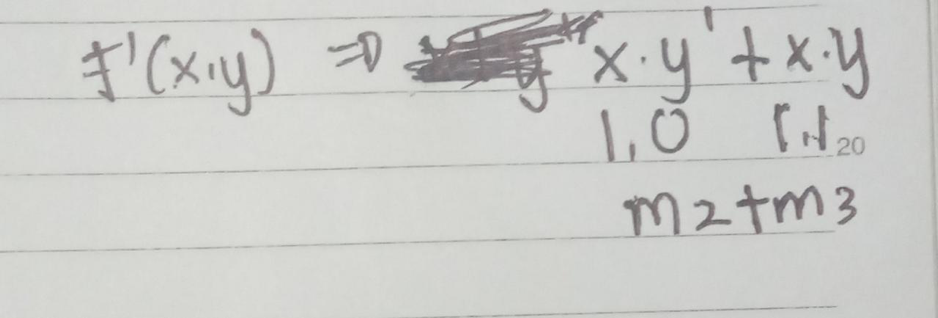

Setelah kita mendapatkan f’(x,y) = xy + xy’, Bentuk fungsi boolean tersebut bukan merupakan bentuk POS namun bentuk SOP, Untuk itu untuk menjadikannya bentuk POS maka kita harus inver-kan lagi, Sehingga menjadi (f’(x,y))’ = (xy + xy’)’, Selanjutnya kita jabarkan menjadi bentuk POS yaitu perkalian dari penjumlahan menggunakan Hukum De Morgan, Hasil konversinya menjadi (f’(x,y))’ = (x’+y)(x’+y’), Dari situ barulah kita dapatkan bentuk standarnya yaitu f(x,y) = (x’+y)(x’+y’), dan bentuk kanoniknya yaitu f(x,y) = ΠM(2, 3)

