
Terdapat Aturan Bentuk standar dan kanonik,
Yaitu 1, Jika f adalah fungsi Boolean satu variabel maka untuk semua nilai x berlaku, f(x) = f (0) . x’ + f (1) . x
Nomor 2, Jika f adalah fungsi Boolean dua variabel maka untuk semua nilai x berlaku, f(x,y) = f(0,0) . x’y’ + f(0,1) . x’y + f(1,0) . xy’ + f(1,1) . xy,
nomor 3, Jika f adalah fungsi Boolean tiga variabel maka untuk semua nilai x berlaku, f(x,y,z) = f(0,0,0) . x’y’ z’ + f(0,0,1) . x’y’z + f(0,1,0) . x’yz’ + f(0,1,1) . x’yz + f(1,0,0) . xy’z’ + f(1,0,1) . xy’z + f(1,1,0) . xyz’ + f(1,1,1) . xyz,
Perhatikan bahwa untuk satu variable maka hanya ada 1 variable yang di-invers-kan, Untuk dua variable maka hanya ada 2 variable yang di-invers-kan, Dan untuk tiga variable maka hanya ada 3 variable yang di-invers-kan

Nomor 4 untuk aturan bentuk standar dan kanonik yaitu SOP-kan atau POS, kan dari mulai baris pertama/ Misal melakukan Konversi fungsi Boolean ke dalam bentuk minterm (SOP), Jika x = 0, y = 0 dan z = 1, maka langsung SOP-kan menjadi f(x,y,z) = x’y’z, Karena minterm berorientasi ke nilai 1, sehingga x harus diinvers menjadi x’/y harus diinvers menjadi y’, Sedangkan z tidak diinvers-kan karena sudah bernilai 1, Begitupun untuk POS,
Misal melakukan Konversi fungsi Boolean ke dalam bentuk Maxterm (POS)
jika x = 1, y = 0 dan z = 1, maka langsung POS-kan menjadi f(x,y,z) = x’+y+z’, Karena Maxterm berorientasi ke nilai 0, sehingga x harus diinvers menjadi x’/ y tidak diinvers-kan karena sudah bernilai 0, z harus diinvers menjadi 0.
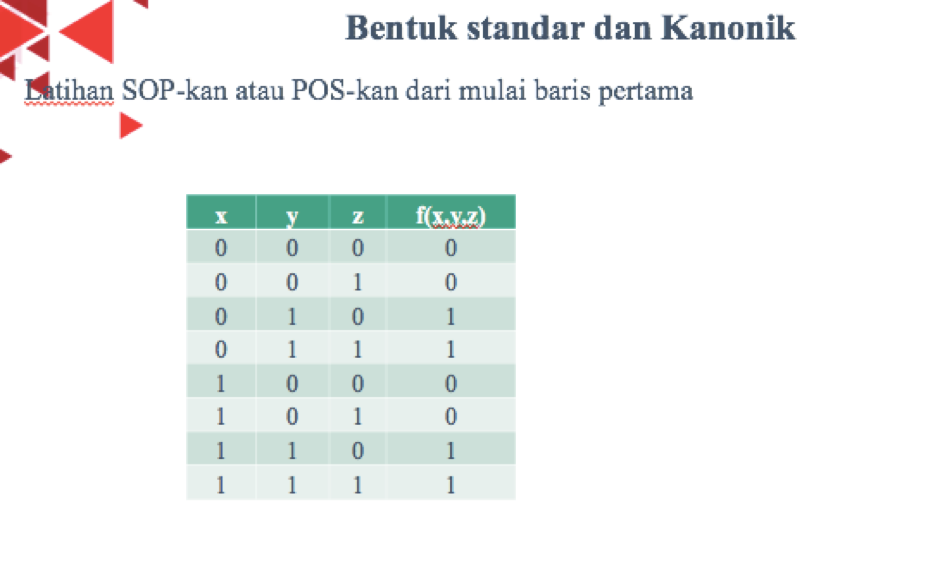
Jika yang diminta ke bentuk minterm (SOP) maka, fokuskan di nilai f(x,y,z) nya yang benilai 1, Sehingga kita dapat hasilkan bentuk minterm nya atau SOP nya, yaitu x’yz ‘+ x’yz + xy’z + xyz, Dan jika yang diminta ke bentuk Maxterm (POS) maka, fokuskan di nilai f(x,y,z) nya yang benilai 0, Sehingga kita dapat hasilkan bentuk Maxterm nya atau POS nya, yaitu (x+y+z)(x+y+z’)(x’+y+z)(x’+y+z’).

