
Konversi fungsi Boolean adalah menyederhanakan suatu fungsi Boolean ke dalam bentuk minterm dan maxterm, Contohnya diketahui hasil akhir fungsi Booleannya yaitu f(x,y,z) = x’y’z + xy’z’ + xyz, Dari contoh fungsi Boolean tersebut nampak bahwa bentuknya adalah SOP (Sum of Product), Penjumlahan dari Perkalian, Maka konversinya ke bentuk minterm, Untuk menjadi bentuk minterm, Yang perlu diingat yaitu bahwa minterm berorientasi pada nilai 1, Sehingga kita harus mencari nilai” dari tabel kebenaran yang berorientasi ke nilai 1, baik untuk variable x, y maupun z, Maka terpilihlah baris 2 atau m yang ke-1 dengan fungsi booleannya x’y’z, Kemudian baris 5 atau m yang ke-4 dengan fungsi booleannya xy’z’, dan baris 8 atau m yang ke-7 dengan fungsi booleannya xyz, Sehingga jika kita gabungkan ketiga fungsi Boolean tersebut mendapatkan konversi fungsi Boolean ke dalam bentuk minterm nya menjadi m1 + m4 + m7, Nampak bahwa SOP terdapat di baris 2, 5 dan 8.

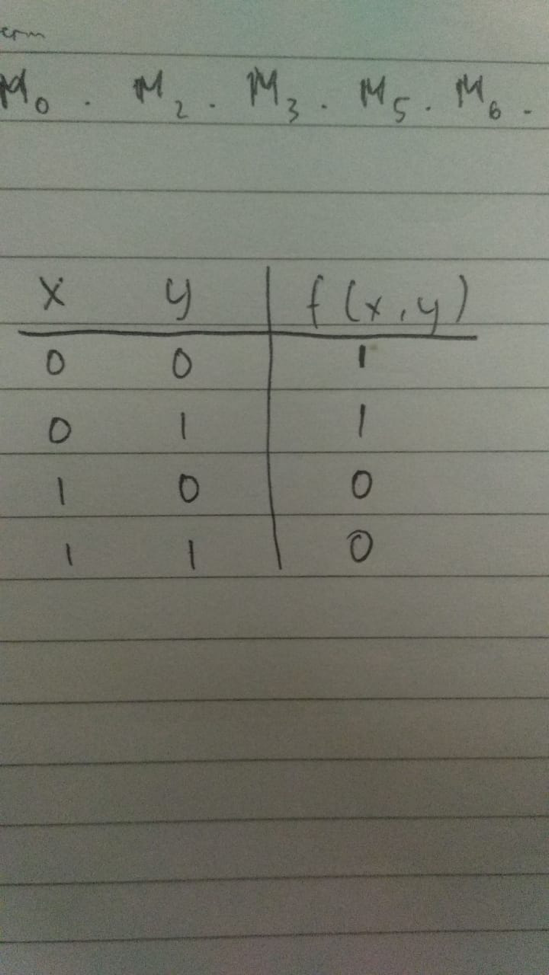
Contohnya diketahui hasil akhir fungsi Booleannya yaitu f(x,y,z) = (x+y+z)(x+y’+z)(x+y’+z’)(x’+y+z’)(x’+y’+z), Dari contoh fungsi Boolean tersebut nampak bahwa bentuknya adalah POS (Product of Sum), Perkalian dari Penjumlahan, Maka konversinya ke bentuk Maxterm, Untuk menjadi bentuk Maxterm, Yang perlu diingat yaitu bahwa Maxterm berorientasi pada nilai 0, Sehingga kita harus mencari nilai” dari tabel kebenaran, baik untuk variable x, y maupun z, Maka terpilihlah baris 1 atau M yang ke-0 dengan fungsi booleannya (x+y+z), Kemudian baris 3 atau M yang ke-2 dengan fungsi booleannya (x+y’+z), baris 4 atau M yang ke-3 dengan fungsi booleannya (x+y’+z’), baris 6 atau M yang ke-5 dengan fungsi booleannya (x’+y+z’), dan baris 7, Sehingga jika kita gabungkan kelima fungsi Boolean tersebut mendapatkan konversi fungsi Boolean ke dalam bentuk Maxterm nya menjadi M0 M2 M3 M5 M6, Nampak bahwa POS terdapat di baris 1, 3, 4, 6, dan 7

Katakanlah hasil akhirnya yaitu f(x,y,z) = x’y’z + xy’z’ + xyz, inversi disini yaitu kita melakukan komplemen terhadap hasil akhirnya, Yang dalam hal ini minterm nya, Maka di dapatlah baris 1 atau M yang ke-0 dengan fungsi booleannya f’(x,y,z) = x’y’z’ + x’yz’ + x’yz + xy’z + xyz’

