Kardinalitas
Menyatakan banyaknya anggota suatu himpunan berhingga
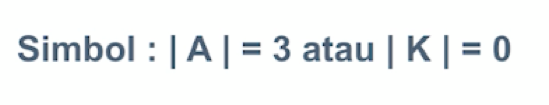
yang dimaksud gambar diatas adalah, jumlah anggota A juga disebut kardinalitas dari himpunan A
|A| = 3 yang artinya jumlah anggota dari himpunan A berjumlah 3
|K| = 0 yang artinya jumlah anggota dari himpunan K berjumlah 0

{} = kurung awal buka kurung awal tutup
{ = kurung awal buka
} = kurung awal tutup
o coret = himpunan kosong
Himpunan Khusus
Himpunan yang mempunyai symbol yang sudah standar
- Himpunan Semesta (Simbolnya S atau U), dinamakan himpunan semesta karena sudah pasti anggotanya lebih banyak dari himpunan-himpunan yang lainnya
Contoh :
1. Himpunan huruf vokal.
S = {A,I,U,E,O}
2. Himpunan bilangan bulat kurang dari 10.
S = {1,2,3,4,5,6,7,8,9}
3. Himpunan faktor dari 12.
S = {1,2,3,4,6,12}
4. Himpunan bilangan prima kurang dari 20.
S = {2,3,5,7,11,13,17,19}
5. Himpunan faktor prima dari 12.
S = {2,3}
himpunan mahasiswa telyu (Himpunan Semesta), kemudian himpunan-himpunan yang didalamnya yaitu himpunan mahasiswa ilmu terapan dan himpunan mahasiswa d3 rpla.
Jumlah himpunan semesta pastinya lebih banyak dibanding jumlah kedua himpunan yang dibawahnya.
- Himpunan Kosong / Null Set (Simbolnya {} atau o coret (himpunan kosong)), adalah himpunan yang tidak memiliki anggota.

| = sedemikian sehingga
< = kurang
> = besar
dari gambar diatas jumlah anggotanya tidak ada, karena, dari notasinya terlihat “tidak ada yang lebih kecil dibanding angkanya dia sendiri”, yang harus diingat dalam himpunan kosong adalah anggotanya tidak ada. Jangan sampai menyebutkan bahwa anggota himpunan kosong atau nol.
Contoh :
4) himpunan nama hari yang dimulai dengan huruf O
karena tidak ada nama hari yang dimulai dengan huruf O, maka himpunan ini disebut himpunan kosong
1) himpunan siswa SMP yang berusia 40 tahun
karena tidak ada siswa SMP yang berusia 40 tahun, maka himpunan ini disebut himpunan kosong
- Himpunan Bagian Sebenarnya / Proper Subset, himpunan bagian dibagi menjadi 2 yaitu himpunan bagian sebenarnya dan himpunan bagian tak sebenarnya.
Mendeskripsikan : A merupakan suatu himpunan dan juga adalah subset dari himpunan B jika dan hanya jika setiap anggota himpunan A juga merupakan anggota himpunan B
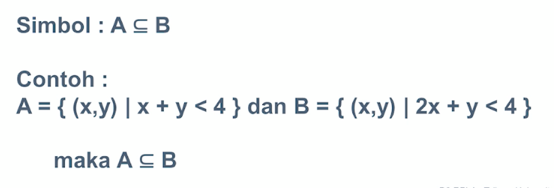
maksud dari gambar diatas adalah : A adalah kurung awal buka x koma y sedemikian sehingga x ditambah y kurang dari 4 kurung awal tutup dan B adalah kurung awal buka x koma y sedemikian sehingga 2x ditambah y kurang dari 4 kurung awal tutup.
- Himpunan Bagian Tak Sebenarnya / Improver Subset, mempunyai himpunan kosong di masing-masing himpunan nya dan jumlah kedua anggota himpunan tersebut yang dibandingkan bisa sama bisa berbeda

gambar diatas maksudnya himpunan kosong subset A dan A subset A
C = Subset
Contoh :
Misalkan himpunan B anggotanya 1,2,3,4 dan C anggotanya 1,2,3,4,5. Contoh himpunan yang tak sebenarnya adalah anggota himpunan B yaitu himpunan kosong 1,2,3,4 dan anggota himpunan C yaitu himpunan kosong 1,2,3,4,5. Dalam hal ini jumlah kedua himpunan tersebut berbeda.
- Himpunan Yang Sama, himpunan A dikatakan sama dengan himpunan B jika dan hanya jika setiap anggota himpunan A merupakan anggota himpunan B dan sebaliknya setiap anggota himpunan B juga merupakan anggota himpunan A.

<-> = sedemikian sehingga
symbol yang digunakan adalah “=”
yang dimaksud pada gambar diatas adalah : A sama dengan B A subset B dan B subset A.
diketahui A anggotanya 1,2,3,4 dan B anggotanya 1,2,3,4. Kedua himpunan tersebut dikatakan sama karena baik himpunan A maupun himpunan B mempunyai jumlah dan anggotanya sama.
- Himpunan yang Ekivalen, dikatakan himpunan A ekivalen dengan Himpunan B jika dan hanya jika kardinalitasnya dari kedua himpunan tersebut sama.

~ = ekivalen
contoh :
diketahui A anggotanya 1,2,3,4 dan B anggotanya tahu, tempe, terong, toge. Meskipun anggota dari kedua himpunan tersebut tidak sama namun kardinalitasnya / jumlah anggotanya kedua himpunan tersebut sama yaitu berjumlah 4 maka sah, maka 2 himpunan tersebut ekivalen.
- Himpunan Saling Lepas, dikatakan 2 himpunan A dan B saling lepas, jika tidak memiliki anggota yang sama. Simbol yang digunakan adalah tidak sama dengan
Contoh :
Himpunan A = {}

